چکیده
گمان عمومی بر این است که خلاقیت باید قاعدتاً درونداشتی ذاتی باشد که جایی در ژن کسی ذخیره شده است و اگر وی فاقد آن باشد از قریحه خلاقیت بیبهره خواهد بود. این ممکن است به تعریف ما از خلاقیت یا آموختههای رسمی و کلیشهای ما در مدرسه یا دانشگاه وابسته باشد. در این سخن کوتاه به ارائه تعبیری از خلاقیت پرداخته میشود که میتوان آن را دارای نمودی غیرذاتی و قابل یادگیری دانست. قلمرو منطقی ریاضیات، درعینحال که ممکن است خاطرهای ناخوشایند از دوران تحصیل را در ما زنده کند، میتواند بستری مناسب برای بارور کردن خلاقیت آموختنی تلقی شود. ما سعی میکنیم گوشهچشمی به این قلمرو داشته باشیم.

مقدمه
وقتی صحبت از ریاضیات میشود ناخودآگاه به یاد محاسبات پیچیده، فرمولهای عجیبوغریب، مشقهای طاقتفرسا و نوشتههایی میافتیم که درک آنها بهسختی ممکن بود. این شاید به دلیل آن باشد که ما در اولین جلسه معارفه با ریاضی در دوران کودکی، حس خوبی از این آشنایی نداشتهایم.
مسئله مهم این است که ما در آشنایی مدرسهای و دانشگاهی با ریاضیات، بیشتر با ریاضیات محاسباتی برخورد میکنیم و یک روی این سکه را ملاقات میکنیم. در کنار این وجه، روی دیگر سکه ریاضی حاوی موضوعات منطقی و غیرمحاسباتی قابلتوجهی است که آکنده از ابتکار، خلاقیت، ژرفنگری و نکتهسنجی است. روی دوم سکه ریاضیات میتواند بستری مناسب برای تمرین خلاقیتی آموختنی باشد. بهعلاوه در همین وجه است که میتوانیم مهارت حل مسئله خود را تقویت کنیم؛ چیزی که به نظر میرسد با ظهور سلسله هوش مصنوعیان بیشتر بدان نیازمند خواهیم بود. چرا که ظاهراً در دنیای آینده شرط لازم برای ادامه حیات در زمینههای اقتصادی، تجاری، بازرگانی، اجتماعی و مواردی از این دست، این است که ما به توانمندسازی هوش طبیعی خود برای مواجه شدن با چالشهای ناشناخته دنیا فردا پرداخته باشیم.
رویکرد منطقی ریاضیات از این جهت مهم است که حاوی انبوهی از مثالهای خلاقانه و ترفندهای ابتکاری برای یادگیری و شبیهسازی خلاقیت است. به رغم آنچه سابق بر این تصور میشد، درک و بازسازی خلاقیت، نه امری ذاتی بلکه مهارتی اکتسابی است. بیتردید همه ما قبول داریم که بر چکاد نشستن در هر رقابتی، نیازمند خلق ایدههای نو، جذاب، شدنی و بکر است. در دنیای امروز که نهتنها علم، بلکه تجارت و بازرگانی نیز بر لبه باریکی از فضاهای واقعی اجتماعی و شبکههای مجازی حرکت میکند، موضوع خلق ایدههای نو امری اجتنابناپذیر مینماید.
پیش از آنکه به چگونگی آموختن خلاقیت بپردازیم، نگاهی اجمالی به مفهوم عرفی خلاقیت خواهیم داشت و پسازآن با ذکر مثالهایی ساده از معماها و بازیهای منطقی، قصد داریم مسیر رسیدن به خلاقیت از طریق یادگیری ریاضی را روشن سازیم.
مفهوم عرفی خلاقیت
ظاهراً مفهوم رسمی خلاقیت به معنای خلق کردن و از هیچ به وجود آوردن است، اما اگر مردم خلاقیت را به این مفهوم برداشت میکردند، آنگاه هیچکسی را نمیتوانستیم خلاق بدانیم؛ چرا که طبق آنچه عموم بدان معتقدند کسی نمیتواند چیزی را از هیچ به وجود آورد.
بااینحال به نظر میرسد که برداشت عرف از کلمه خلاقیت نه به معنای از هیچ به وجود آوردن بلکه به معنای از جایی دور آوردن است. هرچه ایدهای دورتر استفاده شود خلاقانهتر مینماید.
وقتی ما یک وسیله را میبینیم و آن را اختراعی خلاقانه میپنداریم، به این معناست که ما تابهحال آن را برای این منظور به کار نبرده بودیم. تصور کنید به یک نجار، وسایل نجاری بسیار پیشرفته و چوب مرغوب بدهند و از او بخواهند که یک میز درست کند. اگر او یک میز زیبا بسازد، ما صرفاً آن را یک میز شیک و نه لزوماً خلاقانه میپنداریم. اما اگر این نجار یک درِ کهنه را برش بزند و با آن صفحه میز را بسازد و با استفاده از یک صندلی قدیمی که گوشه انباری افتاده بوده پایههای میز خود را جور کند، ما با مشاهده آن میز ناخودآگاه میگوییم چه خلاقیتی داشته! اصلاً گمان نمیرفت که با این وسایل بلااستفاده چنین میزی را خلق کند.
ایدههای خلاقانه معمولاً از جاهای دور و غیرقابلانتظار میآیند. ازاینرو شاید بهتر باشد که به جای کلمه خلاقیت از واژه «نابجاآوری» استفاده کنیم؛ به این معنی که آن ایده از جایی دیگر به اینجا آورده شده و گرچه قبلاً وجود داشته و خلق نشده است، اما به شکلی شگفتآور در اینجا ظاهر شده است.
نکته بعدی این است که معمولاً خلاقیت در کمبود امکانات، تجهیزات و مفروضات رخ میدهد. ازاینرو معمولاً چالشهایی که نیازمند مهارت حل مسئله هستند در رده مسائلی قرار میگیرند که با مفروضات کمتر انتظار نتیجهای عمیقتر و وزینتر را دارند.
معماهای منطقی
یک تمرین ساده برای کسب مهارت حل مسئله بهمنظور یادگیری خلاقیت، این است که ذهن را درگیر معماهای منطقی کنیم.
منظور از معمای منطقی، سؤالی است که پاسخ آن نه با سعی و خطا، بلکه با بررسی منطقی مسئله امکانپذیر است. یکی از راههای بررسی منطقی، این است که ببینیم انجام چه کارهایی ما را به نتیجه مطلوب نخواهد رساند؛ چرا که پیدا کردن پاسخ درست در بین انبوهی از ایدهها که به ذهن متبادر میشود، معمولاً کاری سخت است اما کنار گذاشتن ایدههای نادرست راحتتر صورت میپذیرد.
اجازه دهید برای روشن شدن موضوع، چند مثال را موردبررسی قرار دهیم:
• وصل کردن عددهای یکسان
میخواهیم در شکل زیر عددهای یکسان را با خطوطی (مستقیم یا منحنی) در داخل شکل دوبدو به هم وصل کنیم بهطوریکه خطوط رسم شده یکدیگر را قطع نکنند. آیا این کار ممکن است؟
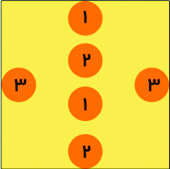
ممکن است فکر کنید که این کار امکانپذیر نیست. مثلاً استدلالی که به ذهن میرسد این است که اگر بخواهیم دو عدد ۳ را به هم وصل کنیم، خطی شکل میگیرد که مربع را به دو قسمت مجزا تقسیم میکند. پس چگونه امکان دارد که بتوانیم عددی در نیمه بالایی را به نظیر آن در پایین متصل کنیم؟
این گرچه استدلالی غلط و گمراهکننده است ولی میتواند نکتهای آموزنده در خود داشته باشد: کاری که نباید بکنیم وصل کردن دو تا ۳ به یکدیگر در قدم اول است. شاید بهتر باشد این کار را به آخر موکول کنیم.
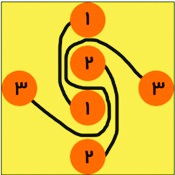
حال شاید حل مسئله دیگر سخت نباشد. ابتدا دو عدد ۱ و دو عدد ۲ را با خطوطی به هم وصل کنید و پسازآن سعی کنید راهی برای متصل کردن دو تا ۳ به یکدیگر پیدا کنید.
• درست کردن ۴ مثلث
میخواهیم با استفاده از ۶ چوب کبریت، ۴ مثلث متساویالاضلاع بسازیم که اندازه هر ضلع آنها برابر با یک چوب کبریت باشد. آیا این کار امکانپذیر است؟
یک استدلال ساده نشان میدهد که برای ۴ مثلث که هر کدام ۳ ضلع دارند ما باید ۱۲ چوب کبریت داشته باشیم. پس ۶ چوب کبریت کم داریم؛ مگر این که هر کدام از چوب کبریتها نقش ضلع دو مثلث را به طور همزمان ایفا کنند.
اگر سعی کنیم روی کاغذ این کار را انجام دهیم با چند آزمایش ساده متوجه میشویم که امکان ندارد ۴ مثلث در مجاورت هم داشته باشیم که هر ضلع آنها در دو مثلث ظاهر شده باشد.
شاید مشکل در اینجاست که ما قصد داریم مسئله را روی کاغذ حل کنیم. اما آیا واقعاً مسئله از ما خواسته است که شکلی روی کاغذ رسم کنیم؟ مسئله به ما چوبکبریت داده و از ما خواسته که مثلثها را «بسازیم». این نباید شکلی سهبُعدی را در ذهن ما مجسم کند؟
چنانچه ما از کاغذ بیرون برویم و کمی دورتر در اجسام سهبُعدی به دنبال جواب باشیم، شاید چندان دور از ذهن نباشد که هرمی با ۴ وجه مثلثی شکل را در نظر بگیریم. کافی است ۳ چوب کبریت را روی زمین به صورت مثلث قرار دهیم و با ۳ چوب کبریت دیگر هرم خود را تکمیل کنیم.
• سرخ کردن ماهیها
ما ۱۰ ماهی داریم که میخواهیم آنها را در یک ماهیتابه با ظرفیت ۴ ماهی سرخ کنیم. برای سرخ کردن یک طرف این ماهیها ۳ دقیقه زمان لازم داریم و برای سرخ کردن طرف دیگر هم ۳ دقیقه. کلاً چند دقیقه زمان لازم دارید تا هر دو طرف همه ماهیها را سرخ کنید؟ (از زمان لازم برای جابجا کردن ماهیها صرفنظر میکنیم.)
اولین راهی که به نظر میرسد (که شاید لزوماً بهترین راه نباشد) این است که هر دو طرف ماهیهای ۱، ۲، ۳، ۴ را در ۶ دقیقه سرخ کنیم و سپس هر دو طرف ماهیهای ۵، ۶، ۷، ۸ را در ۶ دقیقه سرخ کنیم و پس از آن ۶ دقیقه برای سرخ کردن دو طرف ماهیهای ۹ و ۱۰ زمان صرف کنیم. بهاینترتیب ۱۸ دقیقه زمان لازم داریم. اما آیا این کار بهصرفه است؟
بعضی از افراد وقتی چنین مسئلهای را میشنوند به فکر تکه کردن ماهیها، قرار دادن بیش از ۴ ماهی در ماهیتابه، نصف کردن دو ماهی آخر که هر دو طرف در یک بار سرخ شود و راههایی از این دست میافتند اما به نظر نمیرسد پاسخ منطقی این معما، چنین راههایی باشد. ما باید به دنبال راهی باشیم که هر بار ماهیتابه را به طور کامل استفاده کنیم.
مثلاً اگر در اولین بار ماهیهای ۱، ۲، ۳، ۴ را قرار دهیم و در دومین بار پشت ماهیهای ۱، ۲ را همراه با دو ماهی جدید ۵ و ۶ در ماهیتابه بگذاریم و در بار سوم پشت ماهیهای ۳، ۴، ۵، ۶ را قرار دهیم، بهاینترتیب با ۳ بار استفاده از ماهیتابه (در ۹ دقیقه) ما توانستهایم ۶ ماهی را به طور کامل سرخ کنیم.
اکنون با صرف زمان ۶ دقیقه دیگر میتوانیم هر دو طرف ماهیهای ۷، ۸، ۹، ۱۰ را سرخ کنیم یعنی در زمان ۱۵ دقیقه کار را به انجام رساندهایم. بدیهی است که کمتر از این امکانپذیر نیست.
• گذاشتن ۱۰ صندلی دور اتاق
ما میخواهیم ۱۰ صندلی را دورتادور یک اتاق بگذاریم بهطوریکه تعداد صندلیهای روی ۴ ضلع با هم برابر باشد. آیا این کار ممکن است؟
یک پاسخ ساده میتواند این باشد که چون ۱۰ مضرب ۴ نیست پس نمیتوان روی ۴ ضلع، به تعداد مساوی صندلی داشت.
اما شاید ما یک چیز را فراموش کرده باشیم: قرار دادن یک صندلی در یک کنج اتاق میتواند باعث شود که این صندلی روی هر دو ضلع شمرده شود!
بهاینترتیب پاسخ آسان است: اگر دو صندلی را در دو کنج اتاق بگذارید، این دو صندلی دو بار به شمار میآیند پس انگار ما اکنون ۱۲ صندلی داریم و در نتیجه میتوانیم کاری کنیم که روی هر ضلع ۳ صندلی قرار گیرد. کافی است مثلاً دو صندلی را در دو کنج مقابل هم بگذاریم و پس از آن ۸ صندلی باقیمانده را در ۴ ضلع تقسیم کنیم یعنی در هر ضلع ۲ صندلی.
نتیجه
خلاقیت را میتوان آموخت. کافی است چند اصل ساده را رعایت کنیم:
• برای یافتن ایده مناسب برای حل یک چالش، به جنبههای آموزنده دورتر فکر کنیم. گاهی اوقات پاسخ سؤالی که در یک جعبه قرار داده شده است باید در بیرون آن جعبه جستجو شود.
مثلاً در معمای درست کردن ۴ مثلث تا وقتی روی صفحه و به شکل مسطح فکر کنیم نمیتوانیم مسئله رو حل کنیم. لازم است به شکلی سهبُعدی که با چوبکبریتها ساخته شود فکر کنیم.
• به جای آن که از سؤال به پاسخ برسیم، بررسی کنیم که کدام یک از ترفندهای موجود برای حل مسائل میتواند ما را به پرسشی مناسب هدایت کند.
مثلاً در معمای گذاشتن ۱۰ صندلی، میتوانیم ایده استفاده از صندلی مشترک بین دو ضلع را به کار ببریم و معمای زیر را طرح کنیم.
معمای کاشتن ۱۰ درخت در ۵ ردیف ۴ تایی
چگونه میتوانیم ۱۰ درخت را طوری بکاریم که ۵ ردیف ۴ تایی از درختها دیده شود؟
دقت کنید که ۵ ردیف ۴ تایی از درختها به ۲۰ درخت نیاز دارد و ما ۱۰ درخت داریم. پس هر درخت باید طوری قرار گیرد که نقش خود را در دو ردیف ایفا کند. کمی فکر کنید و ببینید میتوانید این معما را حل کنید؟
• گاهی اوقات تفکر خلاقانه مبتنی بر حذف کارهایی است که انجام دادن آنها موجب حل مسئله نخواهد شد.
مثلاً در معمای سرخ کردن ماهیها، استفاده از روشی که موجب شود ماهیتابه با کمتر از ۴ ماهی استفاده شود کار درستی نیست.
ذکر معماهای منطقی در این نوشته از آن جهت است که چنین سؤالاتی، پاسخ مشخص روشن دارند و بررسی صحت پاسخ، پس از اطلاع از پاسخ، کاملاً قابل درک است. ازاینروست که میگویند «معما چو حل گشت آسان شود».
به نظر میرسد خلاقیت نیز وقتی آموخته شود آسان میگردد.
تمام حقوق این وب سایت متعلق به انتشارات اتاق بازرگانی، صنایع، معادن و کشاورزی کرمان است.
طراحی و توسعه: شرکت فناوری اطلاعات رایان سپهر ماهان